Von der induktiven zur deduktiven Forschung
Karten 104 - 109
In einem letzten Schritt wird die bisherige induktive Forschung mit deduktiver Forschung kombiniert.
Die Schlussfolgerungen und Hypothesen der induktiven Studie werden in einer deduktiven Studie verwendet, um die Schlussfolgerungen bzw. Hypothesen zu bestätigen oder zu widerlegen.
Die bisherige Arbeit ergab, dass 60°-Winkel und die Winkel des pythagoreischen Dreiecks 3 : 4 : 5 eine zentrale Rolle bei der geometrischen Anordnung der keltenzeitlichen Burgen und alten Kirchen spielen.
In diesem Schritt werden 60°-Winkel über die Strecke zweier Burgen konstruiert, es ergeben sich folgerichtig zwei gleich große gleichseitige Dreiecke.
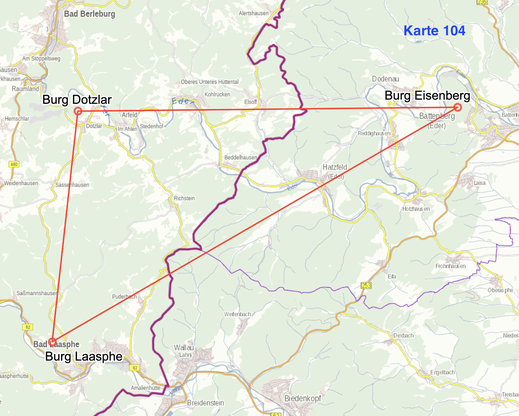
Basis für diese Untersuchung ist die Konstellation Burg Laasphe - Burg Dotzlar - Burg Eisenberg. Konstruiert man über die drei Strecken Burg Laasphe - Burg Dotzlar/Burg Dotzlar - Burg Eisenberg/Burg Laasphe - Burg Eisenberg jeweils gleichseitige Dreiecke mit 60°-Winkeln, ergeben sich sechs Schnittpunkte (S 1 - S 6)
Aufschlussreich sind folgende Winkelgrößen
S 1 - Burg Dotzlar - S 5 106,26° (2 x 53,13°)
S 1 - Burg Dotzlar - S 3 143,13° (90° + 53,13°)
S 1 - Burg Dotzlar - Burg Eisenberg 203,13° (150° + 53,13°)
S 1 - Burg Dotzlar - S 2 120°
S 1 - Burg Dotzlar - S 6 106,26° (2 x 53,13°)
S 1 - Burg Dotzlar - S 4 96,87° (60° + 36,87°)
S 1 - Burg Dotzlar - Burg Laasphe 60°
S 5 - Burg Dotzlar - Burg Eisenberg 96,87° (60° + 36,87°)
S 5 - Burg Dotzlar - S 2 133,74° (60° + 73,74°)
S 5 - Dotzlar - S 6 147,48° (4 x 36,87°)
S 5 - Dotzlar - S 4 156,87° (120° + 36,87°)
S 5 - Burg Dotzlar - Burg Laasphe 193,74° (120° + 73,74°)
S 3 - Burg Dotzlar - Burg Eisenberg 60°
S 3 - Burg Dotzlar - S 2 96,87° (60° + 36,87°)
S 3 - Burg Dotzlar - S 6 110,61° (3 x 36,87°)
S 3 - Burg Dotzlar - S 4 120°
S 3 - Burg Dotzlar - Burg Laasphe 156,87° (120° + 36,87°)
Burg Eisenberg - Burg Dotzlar - S 2 36,87°
Burg Eisenberg - Burg Dotzlar - S 6 50,61° (50,61° + 60° = 110,61° = 3 x 36,87°)
Burg Eisenberg - Burg Dotzlar - S 4 60°
Burg Eisenberg - Burg Dotzlar - Burg Laasphe 96,87° (60° + 36,87°)
S 2 - Burg Dotzlar - S 6 13,74° (13,74° + 60° = 73,74°)
S 2 - Burg Dotzlar - S 4 23, 13° (23,13° + 30° = 53,13°)
S 2 - Burg Dotzlar - Burg Laasphe 60°
S 6 - Burg Dotzlar - S 4 9,39° (9,39° + 60° = 69,39° + 90° = 159,39° = 3 x 53,13°)
S 6 - Burg Dotzlar - Burg Laasphe 46,26° (46,26° + 60° = 106,26° = 2 x 53,13°)
Entsprechende Berechnungen kann man mit den Schnittpunkten, Burg Laasphe und Burg Eisenberg durchführen.
Bezüglich Burg Eisenberg ist ein Aspekt besonders erwähnenswert.
S 3 - Burg Eisenberg - S 5 30°
S 5 - Burg Eisenberg - Burg Dotzlar 30°
Burg Dotzlar - Burg Eisenberg - Burg Laasphe 30°
Burg Laasphe - Burg Eisenberg - S 4 30°
S 4 - Burg Eisenberg - S4 30°

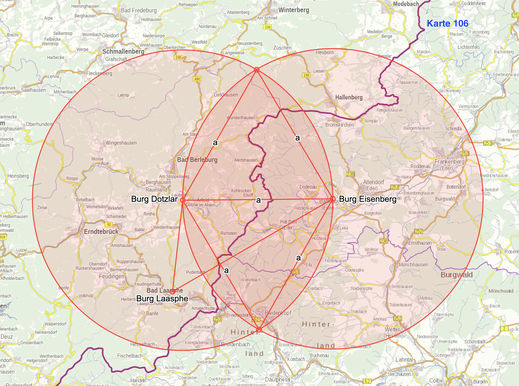
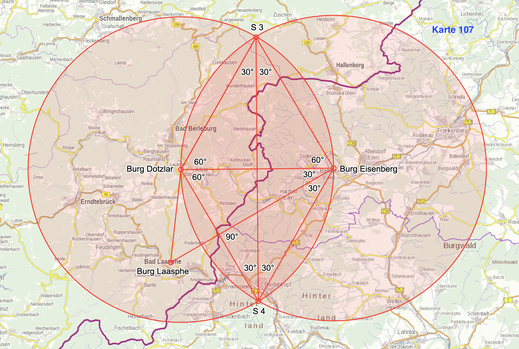
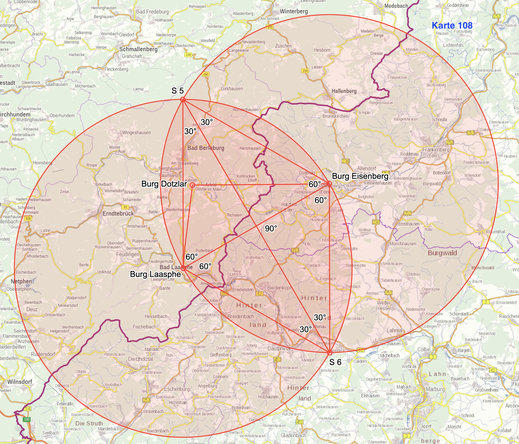
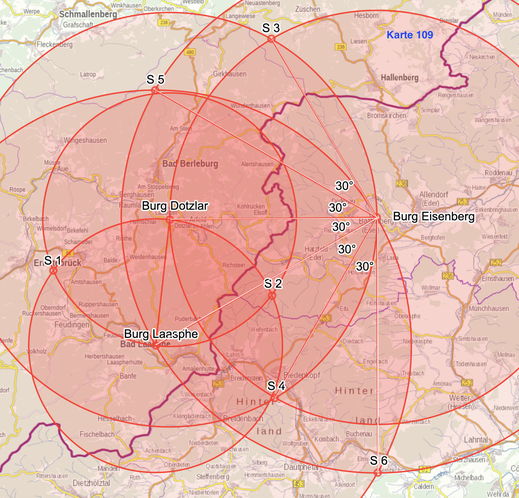
Der Raum westlich von Burg Eisenberg wurde m. H. der Schnittpunkte systematisch strukturiert. Gleich groß sind z. B. die Konfigurationen
Burg Eisenberg - S 4 - Burg Laasphe
Burg Eisenberg - Burg Laasphe - Burg Dotzlar
Burg Eisenberg - Burg Dotzlar - S 5
Burg Eisenberg - S 5 - S 3.
Die Winkel sind jeweils 30° - 53,13° -96,87° (60° + 36,87°).
Auffällig sind auch die beiden gleich großen Dreiecke S 1 - Burg Dotzlar - S 5 und Burg Dotzlar - S 5 - S 3 mit den Winkeln 36,87° - 106,26° - 36,87°.
ohne Karten
Intensiv untersucht wurden bisher die Konstellationen um Burg Dotzlar/Kirche Raumland, Burg Laasphe/Kirche Feudingen und Burg Obernau/Kirche Erndtebrück, wobei die Kirche Erndtebrück nur am Rande mit den übrigen beiden Bereichen verknüpft wurde.
Die Resultate zu den Konstellationen der Kirche Raumland sind in der Einführung auf den Karten 7, 20 - 25, 54, im Kapitel Vertiefungen auf den Karten 77 - 83 dokumentiert.
Die Bezüge der Kirche Erndtebrück sind in der Einführung auf den Karten 38 - 41 dargestellt,
die der Kombination Burg Laasphe - Kirche Feudingen auf den Karten 42 - 44.
Die hypothetische Annahme ist die, dass auch die Kirche Erndtebrück in vieler Hinsicht Teil des Systems ist.
Genau diesen Sachverhalt bestätigen diesbezügliche Berechnungen. Die Daten sind großenteils frappierend exakt, wie die folgende Tabelle ausweist.
Leitlinie ist die im Vorfeld erkannte Verbindung Oppidum Amöneburg - Burg Dotzlar/Kirche Raumland. Die Verlängerung exakt durch die Kirche Raumland erreicht die alte Kirche Wingeshausen, die bisher nicht ins Blickfeld rückte.
Burg Dotzlar - Kirche Wingeshausen - Burg Wilzenberg
127,27° (126,26°)
Burg Dotzlar - Burg Wilzenberg - Kirche Wingeshausen
36,67°(36,87°)
Burg Wilzenberg - Burg Dotzlar - Kirche Wingeshausen
36,06° (36,87°)
Die Konfiguration Burg Dotzlar - Kirche Wingeshausen - Burg Wilzenberg setzt sich aus zwei Dreiecken 3 : 4 : 5 zusammen.
Oppidum Amöneburg - Kirche Raumland - Kirche Puderbach 29,99°(30°)
Oppidum Amöneburg - Kirche Wingeshausen - Burg Laasphe
30,03° (30°)
Die beiden Strecken verlaufen absolut parallel.
Entfernung Kirche Wingeshausen - Burg Wilzenberg 9.749 m
Entfernung Kirche Wingeshausen - Burg Dotzlar 9.890 m
Die Kirche Wingeshausen ist gleich weit von Burg Wilzenberg und Burg Dotzlar entfernt.
Entfernung Kirche Erndtebrück - Burg Dotzlar 11.141 m
Entfernung Kirche Erndtebrück - Burg Laasphe 11.222 m
Die Kirche Erndtebrück ist gleich weit von Burg Dotzlar und Burg Laasphe entfernt.
Kirche Wingeshausen - Kirche Erndtebrück - Burg Laasphe
105,85° (106,26°)
Kirche Wingeshausen - Kirche Feudingen - Burg Laasphe
106,04° (106,26°)
Kirche Feudingen - Kirche Erndtebrück - Kirche Raumland
74,28° (73,74°)
Burg Laasphe - Kirche Erndtebrück - Kirche Raumland
57,84° (57,48° + 90° = 147,48°: 4 = 36,87°)
Kirche Wingeshausen - Kirche Raumland - Burg Laasphe
127,05° (126,87°)
Karten 110 - 112
Eine zentrale Rolle im postulierten Vermessungssystem spielen offensichtlich Quadratraster bzw. die Seitenverhältnisse 1 : 1. Kaum in Erscheinung traten bisher die in diesem Kontext obligatorischen 45° - Winkel. Diese werden beispielhaft über das deduktive Verfahren ermittelt und auf drei Karten und einem Schema präsentiert.
Auffallend genau ist die Konstellation Kirche Wormbach - Kirche Erndtebrück - Kirche Girkhausen (ohne Karte).
Kirche Wormbach - Kirche Erndtebrück 180,27° (180°)
Kirche Erndtebrück - Kirche Wormbach 0,27° (0°)
Kirche Wormbach - Kirche Erndtebrück - Kirche Girkhausen 45,02° (45°)
Die Entfernung Kirche Erndtebrück - Kirche Wormbach beträgt mit 19.972 m genau 9 Leugen.
Kirche Wormbach - Kirche Erndtebrück - Kirche Girkhausen ist ein gleichschenkliges Dreieck.
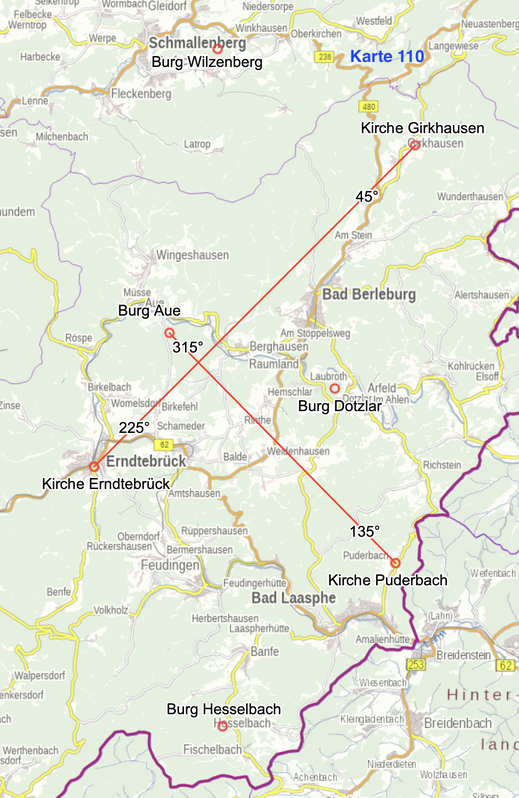
Die Karte zeigt zwei im Zusammenhang stehende Verbindungen, die über 45°- Linien verlaufen. Die Verbindungen orientieren sich an den Haupthimmelsrichtungen.
Die geometrische Position von Burg Dotzlar ist bereits auf den Karten 35 - 37, 89 und 90, 96 - 103 und den Schemata 9 und 10 ausführlich erläutert.
Burg Dotzlar ist ein Musterbeispiel für eine absolut regelhafte Aufteilung des Umfeldes m. H. der Standorte benachbarter Burgen und alter Kirchen.
Karte 111 offenbart zudem eine Orientierung der umliegenden relevanten Bauwerke an nach den Haupthimmelsrichtungen orientierten 45°- Winkeln (45° - 135° - 225° - 315°).
36,87° + 26,565° = 63,435/36,87° + 26,565° + 26,565° = 90°
Die Verlängerungen von Burg Aue-Burg Dotzlar und Kirche Erndtebrück-
Burg Dotzlar Richtung Burghelle würden das Bild komplettieren.
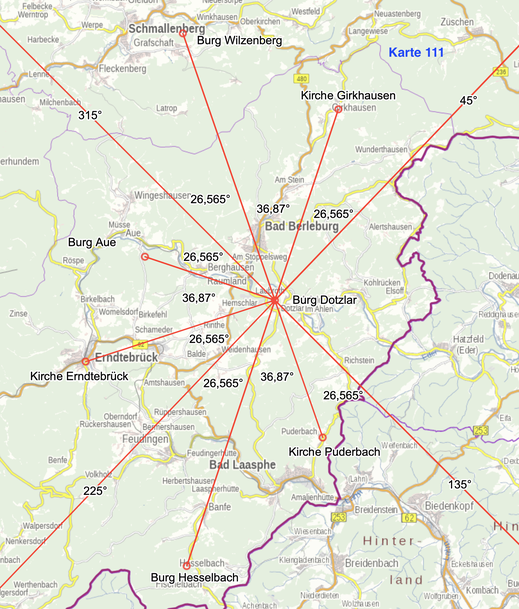

Die Karten 94 und 95 zeigen bereits das Quadratrastersystem. Hier ist auch die im System integrierte Altenburg Römersberg markiert.
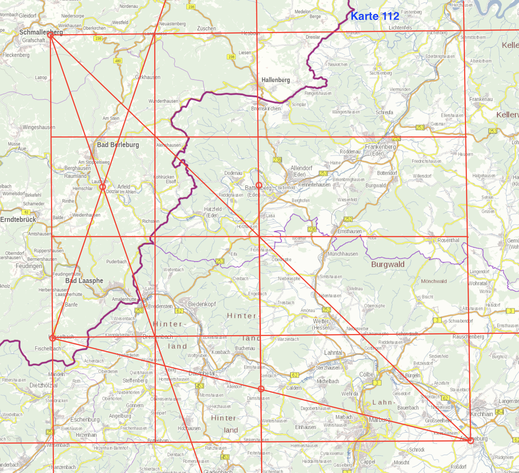
Die Karte 112 und das entsprechende Schema bestätigen wesentliche durch die induktive Erforschung erarbeitete Gesetzmäßigkeiten. Schwerpunkt ist hier, die übergeordneten Gesichtspunkte im Zusammenhang darzustellen.
Das Oppidum Amöneburg und Burg Wilzenberg sind die Eckpunkte eine großen Quadrates mit ca. 40 Kilometer Seitenlänge. Die Burgen Dotzlar, Hesselbach, Eisenberg und Rimberg gliedern den Raum nach dem vorgegebenen Muster.
Das System ist großenteils um etwa 1 Grad nach Nordwesten geneigt.
Die kleinen Quadrate haben eine Seitenlänge von ca. fünf Kilometern bzw. 4,5 Leugen oder 54 Stadien. Weitere Unterteilungen sind vorgegeben.
Folgende Aspekte sind zentral für die Arbeit
- Aufteilung des Raumes in Quadratraster
- Orientierung an den Haupthimmelsrichtungen
- Oppidum Amöneburg als Ausgangspunkt für das Vermessungssystem
- Bestätigung des vermuteten Längenmaßes Leuge bzw. Stadion
- Bestätigung der Funktion der Winkel 18,435° (Seitenverhältnis 1 : 3) - 26,565° (1 : 2) - 14,04° (1 : 4) - 36,87°/53,13° (3 : 4 : 5) - 45° (1 :1)
Letztendlich sind in enger Abfolge noch einmal beweiskräftige Indizien für einen kleinen Raum systematisch zusammengestellt.
Im Mittelpunkt stehen alte Kirchen Wittgensteins und zwei keltenzeitliche Burgen. Kirchen konnten recht genau positioniert werden, entsprechend genau sind die Daten.
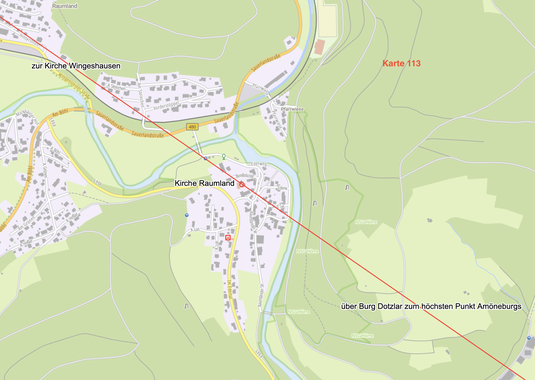
Die Strecke Oppidum Amöneburg (höchster Punkt) - Kirche Wingeshausen
verläuft über Burg Dotzlar und
exakt durch die Kirche Raumland.
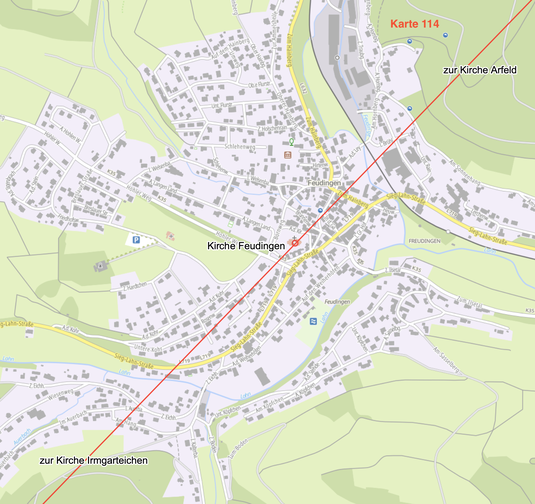
Die Fortführung der Strecke Kirche Irmgarteichen - Kirche Feudingen endet in der Kirche Arfeld.
Auch hier verläuft die Linie exakt durch die Kirche.
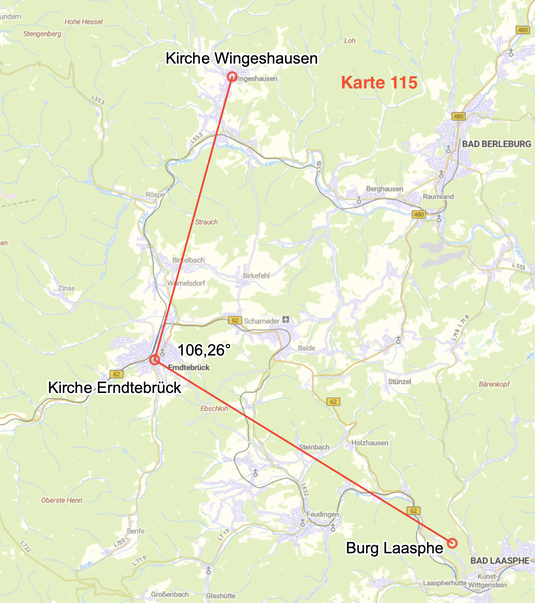
Der Winkel Kirche Wingeshausen - Kirche Erndtebrück - Burg Laasphe ist 106,26° (2 x 53,13°) groß.
Der berechnete Wert ist 105,85°.
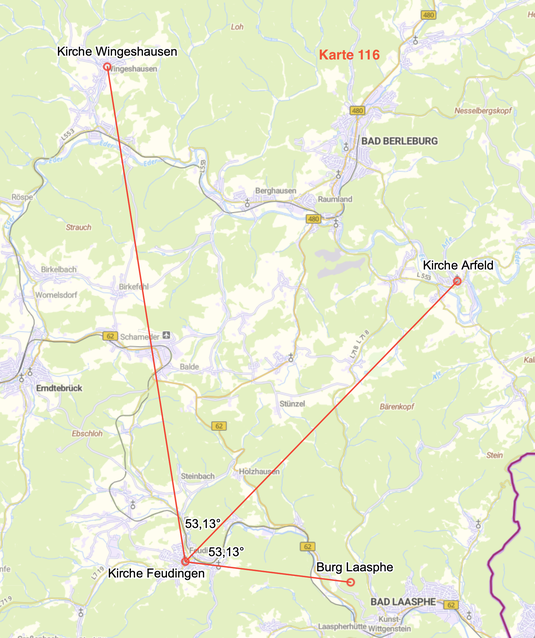
Der Winkel Kirche Wingeshausen - Kirche Feudingen - Burg Laasphe misst ebenfalls 106,26° (106,04°).
Halbiert wird dieser Winkel durch die Strecke Kirche Feudingen - Kirche Arfeld mit je 53,13°
Die berechnete Größe des Winkels Kirche Wingeshausen - Kirche Feudingen - Kirche Arfeld ist 53,05°,
die des Winkels Kirche Arfeld - Kirche Feudingen - Burg Laasphe 52,99°.
Der Winkel Kirche Raumland - Kirche Erndtebrück - Kirche Feudingen ist im Übrigen 73,74° (2 x 36,87°) groß.
Der berechnete Wert ist 74,28°.
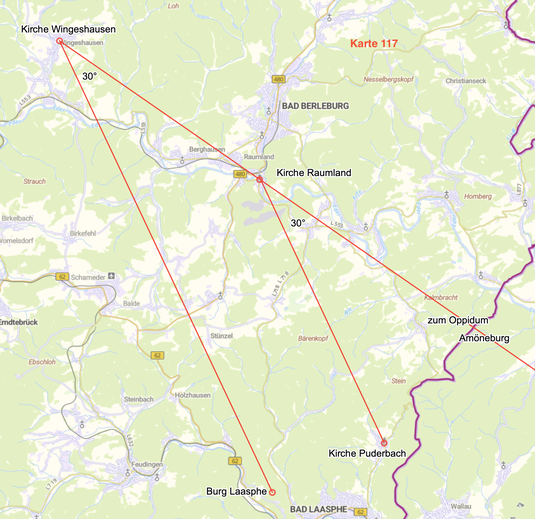
30° groß ist jeweils der Winkel Oppidum Amöneburg - Kirche Raumland - Kirche Puderbach (29,99°) und
Oppidum Amöneburg - Kirche Wingeshausen - Burg Laasphe (30,03°).
Die Strecken Kirche Raumland - Kirche Puderbach und Kirche Wingeshausen - Burg Laasphe verlaufen folglich genau parallel.
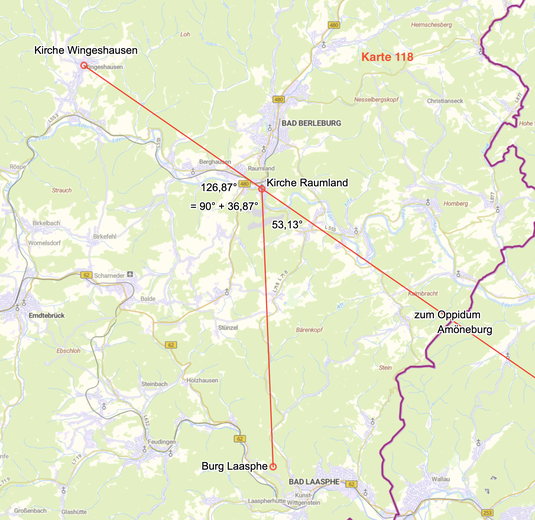
53,13° (52,97°) ist der Winkel Oppidum Amöneburg - Kirche Raumland - Burg Laasphe,
126,87° (127,03°) entsprechend der Winkel Kirche Wingeshausen - Kirche Raumland - Burg Laasphe.
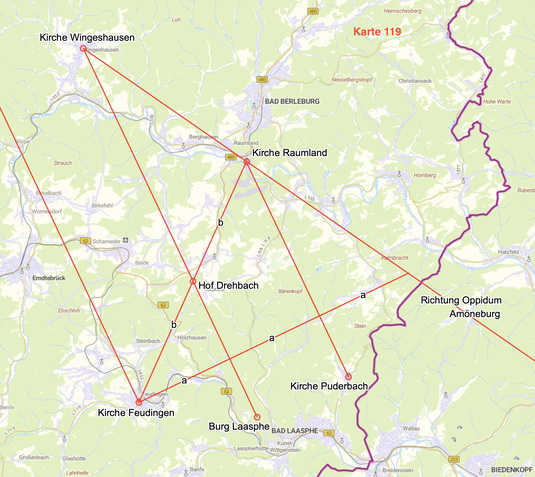
Über dem Konstrukt Oppidum Amöneburg - Kirche Raumland - Kirche Puderbach und Oppidum Amöneburg - Kirche Wingeshausen - Burg Laasphe lässt sich ein perfektes 30°-System konstruieren.
Zu den Parallelen Kirche Raumland - Kirche Puderbach und Kirche Wingeshausen - Burg Laasphe führt eine weitere Parallele mit exakt dem gleichen Abstand durch die Kirche Feudingen.
Die gleichen Distanzen sind mit a gekennzeichnet.
Die Strecke Kirche Raumland - Kirche Feudingen wird genau auf der Verbindung Kirche Wingeshausen - Burg Laasphe halbiert. Der Punkt ist Hof Drehbach. Dieser Ort ist Kreuzungspunkt zweier alter Fernstraßen. Die beiden gleichlangen Strecken sind mit b gekennzeichnet.
Der geometrische Zusammenhang der beiden Urkirchen Raumland und Feudingen ist offensichtlich.
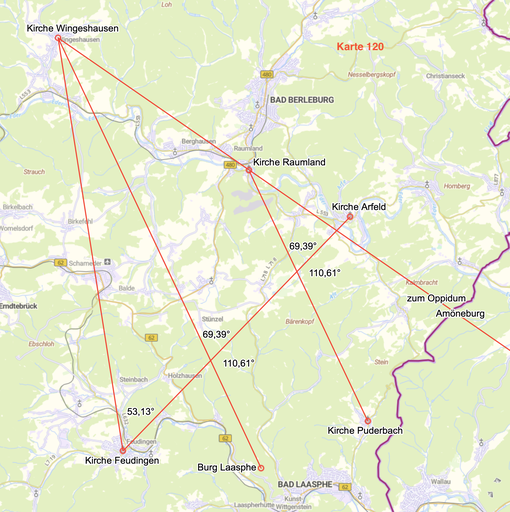
Der Winkel Kirche Wingeshausen - Kirche Feudingen - Kirche Arfeld ist 53,13° (53,05°) groß.
Die Strecke Kirche Feudingen - Kirche Arfeld schneidet die Verbindungen Kirche Wingeshausen - Burg Laasphe und Kirche Raumland - Kirche Puderbach in 69,39°/110,61° - Winkeln.
Durch Anlegen eines 90°- Winkels ergeben sich hier 159,39°- Winkel (69,39° + 90° = 159,39°).
110,61° sind 3 x 36,87°,
159,39° sind 3 x 53,13°.
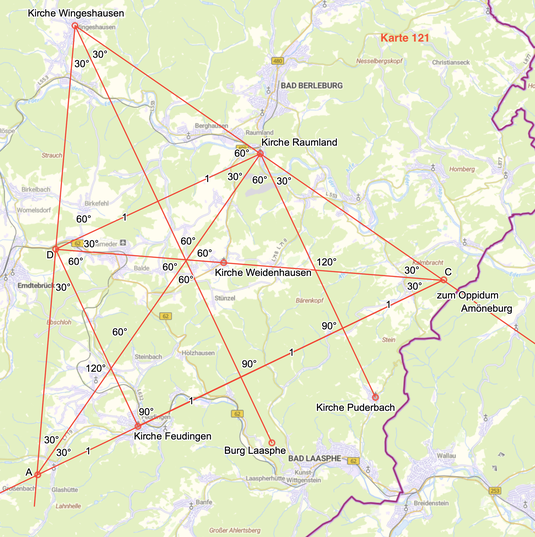
Die Gesetzmäßigkeiten sind noch aufschlussreicher, wenn man das gleichseitige Dreieck A - Kirche Wingeshausen - C über den Kirchen Wingeshausen, Raumland und Feudingen entwickelt.
Aufgedeckt wird ein konsequentes 30°-System.
Die Kirche Raumland halbiert die Strecke Kirche Wingeshausen - C exakt.
A - C wird genau in vier gleichgroße Abschnitte geteilt, A - Kirche Feudingen ist 1/4 der Strecke A - C.
Die Verbindung Kirche Raumland - D ist halb so lang wie A - C.
Die Kirche Weidenhausen liegt exakt auf C - D.
Insgesamt kann dieses Konstrukt als Grundlage für eine systematische Vermessungslandschaft auf der Basis von 30° - Winkeln dienen.
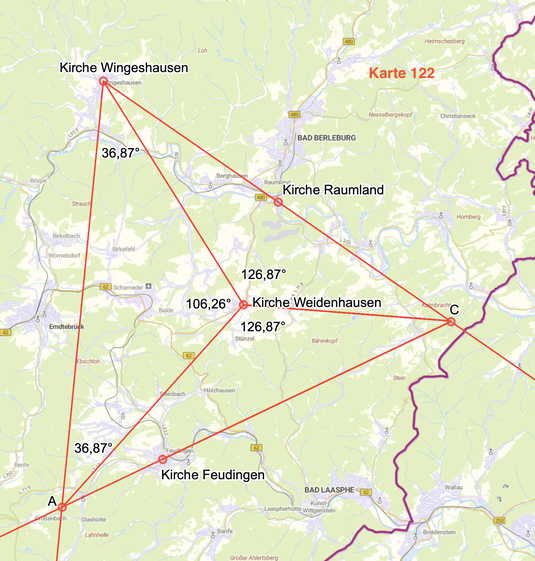
Die Karte zeigt die Funktion der Kirche Weidenhausen innerhalb des gleichseitigen Dreiecks A - Kirche Wingeshausen (B) - C auf.
Das Dreieck A - Kirche Wingeshausen - Kirche Weidenhausen weist die Winkel 36,87° - 106,26° - 36,87° auf,
die Figur A - Kirche Weidenhausen - Kirche Wingeshausen 253,74°.
Die Verbindung Kirche Wingeshausen - C halbiert den Winkel exakt in zwei 126,87° Sektoren.
Über die Fortführungen der Strecken A - Weidenhausen, Wingeshausen (B) - Weidenhausen und C - Weidenhausen sind pythagoreische Dreiecke 3 : 4 : 5 zu konstruieren. Die Kirche Weidenhausen ist der Mittelpunkt dieser Konstruktion.
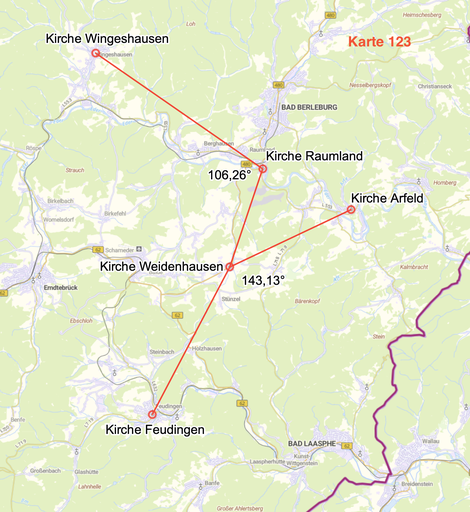
Die Kirche Weidenhausen steht darüber hinaus mit den bedeutenden umliegenden Plätzen in strengem geometrischen Kontakt.
Der Winkel Kirche Wingeshausen - Kirche Raumland - Kirche Weidenhausen misst 106,26° (106,20°), der Winkel Kirche Arfeld - Kirche Weidenhausen - Kirche Feudingen 143,13° (142,96°).
Tabelle (ohne Karte)
20,61°: 180° - 20,61° = 159,39° : 3 = 53,13°
Burg Dotzlar - Kirche Weidenhausen - Kirche Arfeld 20,61° (20,70°)
Kirche Weidenhausen - Kirche Raumland - Burg Laasphe 20,61° (20,85°)
Kirche Feudingen - Kirche Arfeld - Kirche Weidenhausen 20,61° (20,57°)
Kirche Arfeld - Kirche Feudingen - Kirche Weidenhausen 16,26° (16,47°)
Kirche Erndtebrück - Kirche Feudingen - Kirche Weidenhausen 69,39°/69,39° + 150° = 159,39° (69,57°)
Kirche Weidenhausen - Kirche Feudngen - Burg Laasphe 69,39° (69,46°)
Auffallend groß ist auch die Genauigkeit der Winkel um die Kirche Weidenhausen, die sich aus der Kombination von 30°-Winkeln und den Winkeln des pythagoreischen Dreiecks 3 : 4 : 5 zusammensetzen.
Kirche Feudingen - Kirche Weidenhausen - Kirche Raumland 170,61°= 110,61°+60° (berechneter Wert 170,87°)
Kirche Wingeshausen - Kirche Weidenhausen - Kirche Arfeld 96,87°=36,87° + 60° (96,76°)
Kirche Wingeshausen - Kirche Weidenhausen - Kirche Puderbach 163,74° = 73,74° + 90° (163,66°)
Kirche Raumland - Kirche Weidenhausen - Kirche Puderbach 113,13° = 53,13° + 60° (113,07°)
Kirche Puderbach - Kirche Weidenhausen - Kirche Arfeld 66,87° = 36,87° + 30° (66,90°)
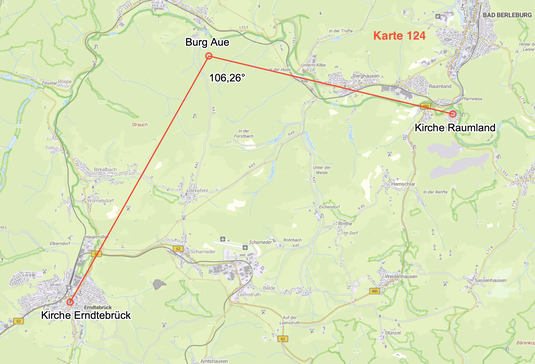
In das Bild passt der Umstand einer engen Verknüpfung zwischen den alten Kirchen und den umliegenden Burgen.
Beispielhaft ist hier Burg Aue aufgeführt.
Aus dem Folgenden geht hervor, dass die Burg offensichtlich zentraler Bezugspunkt für die benachbarten Kirchen war.
Kirche Erndtebrück - Burg Aue - Kirche Raumland 106,26° (105,80°)
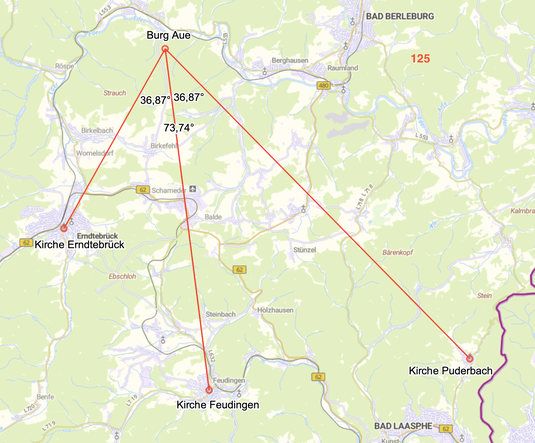
Kirche Erndtebrück - Burg Aue - Kirche Puderbach 73,74° (berechneter Wert 73,83°)
Kirche Erndtebrück - Burg Aue - Kirche Feudingen 36,87° (36,65°)
Kirche Feudingen - Burg Aue - Kirche Puderbach 36,87° (37,18°)
ohne Karte
Kirche Weidenhausen - Burg Aue - Kirche Raumland 36,87° (36,17°)
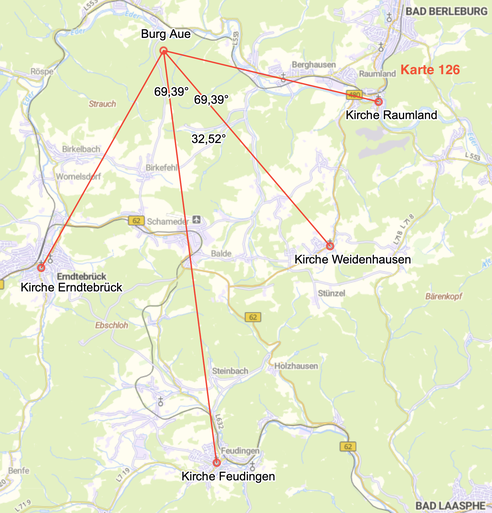
Wesentlich differenziertere Sachverhalte zeigt Karte 126 auf.
Kirche Erndtebrück - Burg Aue - Kirche Weidenhausen 69,39° (berechneter Wert 69,63°)
Kirche Feudingen - Burg Aue - Kirche Raumland 69,39° (69,15°)
Kirche Feudingen - Burg Aue - Kirche Weidenhausen 32,52° (32,98°)
ohne Karte
Kirche Puderbach - Burg Aue - Kirche Raumland 32,52° (31,97°)
69,39° + 90° = 159,39° = 3 x 53,13°
180° - 69,39° = 110,61° = 3 x 36,87°
180° - 32,52° = 147,48° = 4 x 36,87°
180° + 32,52° = 212,52° = 4 x 53,13°
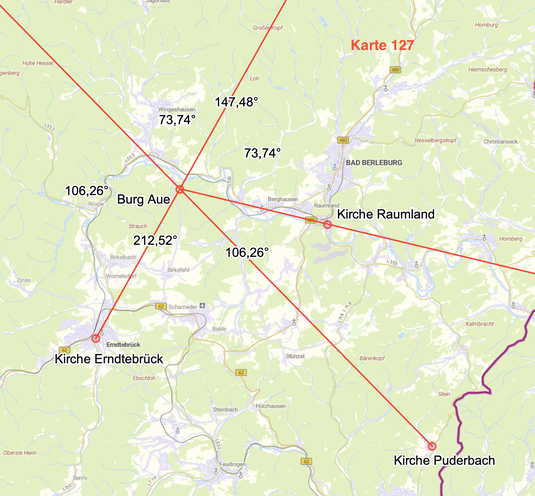
Im Kontext mit den Fortführungen ergibt sich ein perfektes Rundum-System.
Aufgeführt ist das Beispiel
Burg Aue - Kirche Raumland/Fortführung Kirche Puderbach - Burg Aue 147,48°/212,52°
Fortführung Kirche Puderbach - Burg Aue/Burg Aue - Kirche Erndtebrück 106,26°
Burg Aue - Kirche Erndtebrück/Burg Aue - Kirche Raumland 106,26°
Auf Karte 125 ist die Funktion der Kirche Feudingen dargestellt.
Demnach ist Burg Aue - Kirche Raumland/Fortführung Kirche Feudingen - Burg Aue 110,61°,
Burg Aue -Kirche Feudingen/Fortführung Kirche Puderbach - Burg Aue 143,13°.
Folglich wurde um die Burg Aue m. H. der Standorte der alten Kirchen ein perfektes Vermessungssystem auf der Basis der Winkel 36,87°/53,13°/73,74°/106,26° konstruiert.
Koordinaten und Meridiankonvergenzen (Meridiankonvergenzen wenn verwendet)
Oppidum Amöneburg 94500 m : 27198 m 0,06°
Burg Aue 51080 m : 54616 m 0,54°
Burg Burbach 34090 m : 21079 m 0,72°
Burg Christenberg 82332 m : 44846 m 0,2°
Burg Dotzlar 58351 m : 52155 m 0,46°
Oppidum Dünsberg 70330 m : 11008 m 0,32°
Burg Eisenberg 73657 m : 52330 m 0,29°
Burg Hesselbach 53461 m : 37266 m 0,51°
Burg Heunstein 50584 m : 23692 m 0,54°
Burg Hofkühlberg 28205 m : 59663 m 0,80°
Burg Hoher Lehnberg 41036 m : 65309 m
Burg Hunnenburg 94516 m : 20999 m
Burg Jäckelchen 27278 m : 60617 m
Burg Kahle 35358 m : 63727 m 0,72°
Burg Kindelsberg 30075 m : 49176 m
Burg Laasphe 57309 m : 42830 m 0,47°
Burg Obernau 40604 m : 42947 m 0,66°
Burg Rimberg 73901 m : 32372 m 0,29°
Burg Altburg Stein-Wingert 10503 m : 20444 m
Burg Totenberg 85276 m : 14039 m
Burg Weilenscheid 33384 m : 66172 m 0,74°
Burg Wemlighausen 62348 m : 59148 m 0,42°
Burg Wilzenberg 53192 m : 67105 m 0,52°
Kirche Arfeld 60410 m : 51587 m
Kirche Bromskirchen 73713 m : 60437 m
Kirche Dautphe 67737 m : 34091 m
Kirche Erndtebrück 47754 m : 48716 m 0,58°
Kirche Feudingen 52502 m : 43429 m 0,52°
Kirche Girkhausen 61892 m : 62430 m 0,42°
Kirche Irmgarteichen 43531 m : 34174 m
Kirche Puderbach 61028 m : 44463 m 0,44°
Kirche Raumland 56885 m : 53211 m 0,48°
Martinskirche Siegen 31064 m : 36249 m
Kirche Weidenhausen 55576 m : 49300 m
Kirche Wingeshausen 50240 m : 57814 m
Kirche Wormbach 48050 m : 68688 m 0,58°